O Mínimo Múltiplo Comum (MMC) e o Máximo Divisor Comum (MDC) são conceitos fundamentais na matemática básica e são amplamente utilizados na simplificação de frações, resolução de problemas e até na matemática de concursos. Neste artigo, você aprenderá o que são MMC e MDC, a diferença entre eles e como calculá-los com exemplos práticos.
“Se você está se preparando para concursos, veja nossos cursos especializados e acompanhe o canal
Matemática com Emerson para mais conteúdos.”
O que é MMC?
O Mínimo Múltiplo Comum (MMC) entre dois ou mais números é o menor número inteiro que é múltiplo de todos esses números. Em outras palavras, é o menor valor que pode ser dividido igualmente por todos os números do conjunto.
Quando usar o MMC?
O MMC é útil, principalmente, quando precisamos:
- Somar ou subtrair frações de denominadores diferentes.
- Encontrar um padrão em problemas envolvidos múltiplos.
O Que São Múltiplos?
Múltiplos são o resultado da multiplicação de um número por qualquer outro número natural. Eles representam valores que esse número “gera” ao ser multiplicado e são infinitos.
Para encontrar os múltiplos de um número, basta multiplicá-lo por n
- Múltiplos de 5 : 5, 10, 15, 20, 25, 30, …
- Múltiplos de 7 : 7, 14, 21, 28, 35, 42, …
Como Calcular o MMC
Para calcular o MMC entre números, use o método da seleção em fatores primos ou o método dos múltiplos.
Exemplo:
Primeiro, observa-se os múltiplos de 3, 5 e 10:
M(3) = {0,3,6,9,12,15,18,21,24,27,30,…}
M(5) = {0,5,10,15,20,25,30,35,40,45,…}
M(10) = {0,10,20,30,40,50,60,70,80,90,100,…}
Desses múltiplos, então, busca-se os valores que são comuns entre si (interseção): 0, 30,….
M(3) ∩ M(5) ∩ M(10) = {0,30,60,…}
Caso se queira saber os próximos números comuns entre si, basta adicionar 30:
M(3) ∩ M(5) ∩ M(10) = {0,30,60,90,120,…}
Dentre os múltiplos comuns, observa-se, portanto, o menor, excluindo o 0. Dessa forma, tem-se o MMC de 3, 5 e 10:
MMC(3,5,0) = 30
Por esse se tratar de um método lento, também é possível encontrar o MMC por meio de uma fatoração sucessiva. Na esquerda da barra se encontram os números cujo MMC se deseja encontrar, e na direita colocam-se números primos para divisão, da seguinte forma:
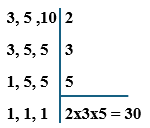
Portanto, o MMC entre 3, 5 e 10 é 30 .
Aqui deixo um vídeo sobre Como fazer MMC.

O que é MDC?
O Máximo Divisor Comum (MDC) entre dois ou mais números é o maior número que divide todos esses números sem deixar resto. Esse conceito é especialmente útil para simplificar frações e resolver problemas de divisão em partes iguais.
Quando usar o MDC?
O MDC é importante quando:
- Queremos simplificar frações ao máximo.
- Precisamos dividir algo em partes iguais.
O Que São Divisores?
Para encontrar os divisores de um número natural, siga estes passos:
- Comece pelo 1 : Todo número natural é divisível por 1 e por ele mesmo, então esses são sempre os primeiros divisores.
- Teste os números sequencialmente : Divida o número pelo 2, depois pelo 3, e assim por diante, até chegar ao próprio número.
- Verifique se a divisão é exata : Se a divisão não deixa resto, o divisor é válido.
Exemplo: Divisores de 18
- 1 divide 18: 18÷1 = 18
- 2 divide 18: 18÷2 = 9
- 3 divide 18: 18÷3 = 6
- 6 divide 18: 18÷6 = 3
- 9 divide 18: 18÷9 = 2
- 18 divide 18: 18÷18 = 1
Então, os divisores de 18 são 1, 2, 3, 6, 9 e 18 .
Como Calcular o MDC
O MDC pode ser calculado usando o método da invenção em fatores primos ou o método da divisão sucessiva .
Exemplo:
Observa-se os divisores de 12, 18 e 24:
D(12) = {1,2,3,4,6,12}
D(18) = {1,2,3,6,9 ,18}
D(24) = {1,2,3,4,6,8 ,12,24}
Desse modo, tem-se que a interseção entre esses divisores (ou seja, o que eles possuem em comum) será:
D(12) ∩ D(18) ∩ D(24) = {1,2,3,6}
Considerando que entre esses divisores comuns o maior é o 6, entende-se então que o MDC é igual a 6. Dessa forma, por MDC entende-se o maior valor que divide os três números ao mesmo tempo.
Também é possível calcular o MDC por meio de divisão sucessiva, porém trabalhando com fator comum no lado direito (que não precisam ser primos):
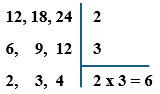
Logo, o MDC entre 12, 18 e 24 é 6 .
Diferença entre MMC e MDC
- MMC : Focado em encontrar o menor múltiplo comum, utilizado principalmente em operações com frações e sequências de múltiplos.
- MDC : Baseado na identificação do maior divisor comum, essencial para simplificação de frações e divisão em partes iguais.
Conclusão
Aprender a calcular o MMC e o MDC é fundamental para resolver muitos problemas matemáticos. Na prática, você dominará esses conceitos, aplicando-os de forma eficaz em frações, divisão de recursos e muito mais. Quer mais dicas e conteúdo prático sobre matemática? Continue acompanhando o blog e compartilhe este artigo!
Baixe o PDF deste artigo Grátis: Baixar PDF
“Gostou do conteúdo?
